The interlink between quantum theory and machine learning

Introduction

Machine learning is a branch of computer science that aims to create programs that can find useful knowledge and make assumptions about data. It’s at the heart of artificial intelligence (AI), and it’s powering anything from facial recognition to natural language processing to automatic self-driving vehicles. Dimensionality is the most challenging machine learning problem; in general, the number of training data sets needed for the machine to learn the desired information is exponential in dimension d. If a data set is located in a high-dimensional space, it becomes computationally uncontrollable. This level of sophistication is comparable to quantum mechanics, where an infinite number of data is needed to explain a quantum many-body state completely. This article will explain the scientific interlink between quantum theory and machine learning.

Quantum neural networks representation

Artificial neural networks (ANNs) are models used in grouping, regression, compression, generative modelling, and statistical inference. The alternation of linear operations with nonlinear transformations (e.g. sigmoid functions) in a theoretically hierarchical manner is their unifying feature. In Quantum Machine Learning (QLM), NNs have been extensively studied [1]. The main research directions have been to speed up classical models’ training and build networks with all constituent components, from single neurons to training algorithms, running on a quantum computer (a so-called quantum neural network).  Along with the rapid development of machine-learning algorithms for determining phases of matter, artificial neural networks have made significant progress in describing quantum states and solving important quantum many-body problems. Completely defining an arbitrary many-body state in quantum mechanics necessitates an exponential number of data.

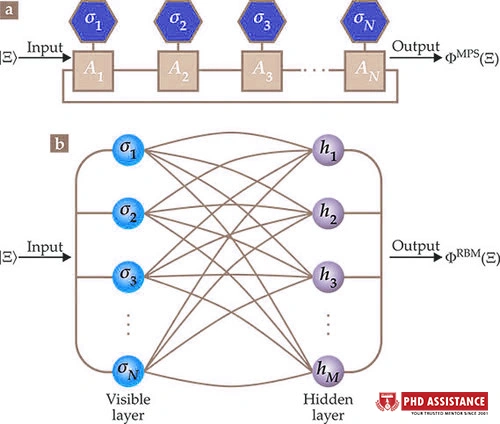
Figure 1. A Quantum neural networks representation [1]

For computational simulations of quantum many-body structures on a classical machine, the exponential difficulty presents a huge challenge—describing even a few qubits necessitates a massive amount of memory. Moreover, only a small part of all Hilbert’s Quantum space, such as the ground states of many-body Hamiltonians, can enter physical states of concern and be depicted with fewer details. Compact models of quantum many-body states must be constructed while maintaining their basic physical properties to solve quantum many-body problems using classical computers. The tensor-network representation [2], in which each qubit is given a tensor, and these tensors together characterise the many-body quantum state, is a well-known explanation for such states. Since the volume of data required is only polynomial instead of exponential, the system’s size is the most accurate description of the physical condition.

Quantum-based machine learning

Most quantum machine learning algorithms necessitate fault-tolerant quantum computing, which necessitates the aggregation of millions of qubits on a wide scale, which is currently unavailable. Quantum machine learning (QML), however, includes the first breakthrough algorithms applied on commercially viable noisy intermediate-scale quantum (NISQ) computers. Many interesting breakthroughs were made at the crossroads of quantum mechanics and machine learning. Machine learning has been successfully used in many-body quantum mechanics to speed up calculations, simulate phases of matter, and find vibrational analysis for many-body quantum states, for example. In quantum computing, machine learning has recently shown performance in quantum control and error correction [3]. Finding the system’s ground state or the dynamics of the system’s time evolution is typically the first step in solving quantum many-body problems. Carleo and Troyer proposed the RBM representation, used an RBM-based variational learning algorithm to do this [4]. They applied the technique to two prototypical quantum spin models: the Ising model in a transverse magnetic field and the antiferromagnetic Heisenberg model.  They discovered that it accurately captured the ground state and time evolution for both [5].

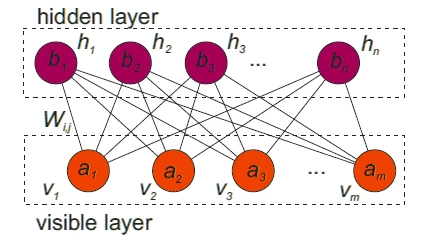
Figure 2. A restricted Boltzmann machine (RBM) is composed of hidden and visible layer [5]

A series of new recent algorithms covering core areas of machine learning (supervised, unsupervised, and reinforcement learning), as well as other quantum-classical data and algorithms (QQ, QC, CQ models), is still to be done. Scaling up the algorithms to the limits of actual hardware while doing an effective scaling study of performances and corresponding errors is important. Finally, one should determine if a quantum speedup using quantum machine learning models operating on NISQ machines is technically and experimentally feasible.

Future scope

In the case of quantum algorithms for linear algebra, where robust guarantees are already possible, data access issues and limitations on the types of problems that can be solved can impede their success in practice. Indeed, developments in quantum hardware growth in the coming future would be critical for empirically assessing the true potential of these techniques. It’s worth noting that the bulk of the QML literature has come from within the quantum culture. Further advancements in the area are expected to arrive only after major contacts between the two cultures. The interdisciplinary field of mixing machine learning and quantum physics is increasingly expanding, with promising results. The points raised above are just the tip of the iceberg.

Reference

[1] Sankar Das Sarma, Dong-Ling Deng, and Lu-Ming Duan, “Machine learning meets quantum physics”, Physics Today 72, 48-54 (2019) https://doi.org/10.1063/PT.3.4164

[2] William Huggins et al 2019 Quantum Sci. Technol. 4 024001

[3] Lorenzo Buffoni and Filippo Caruso 2020 EPL 132 60004.

[3] Kishor Bharti, Tobias Haug, Vlatko Vedral, and Leong-Chuan Kwek, “Machine learning meets quantum foundations: A brief survey”, AVS Quantum Science 2, 034101 (2020) https://doi.org/10.1116/5.0007529

[4] G. Carleo, M. Troyer, Science 355, 602 (2017) https://doi.org/10.1126/science.aag2302

[5] Lee, Chee Kong and Patil, Pranay and Zhang, Shengyu and Hsieh, Chang Yu, Neural-network variational quantum algorithm for simulating many-body dynamics, Phys. Rev. Research, 3, 2021, 023095, DOI: 10.1103/PhysRevResearch.3.023095